문제
난이도: 플레티넘 5
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구해야 한다.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
다음과 같이 가장 긴 증가하는 부분 수열 시리즈가 있다.
LIS (Longest Increasing Subsequence) 알고리즘은 가장 긴 증가하는 부분 수열을 찾는 문제를 해결하는 알고리즘으로 주어진 수열에서 순서를 유지하면서, 원소들이 증가하는 부분 수열 중 가장 긴 수열을 찾아내는 것을 목표로 한다.
만약 해당 알고리즘이 생소하다면 위 시리즈를 순서대로 풀어보는 것을 추천한다.
알고리즘에 대한 설명은 이 영상에서 가장 쉽게 설명하는 것 같아 첫 문제부터 방향이 전혀 잡히지 않는다면 해당 영상을 먼저 보는 걸 권장한다.
풀이 과정
풀이 시간: 1시간 40분
알고리즘: 이분 탐색 + 다이나믹 프로그래밍
수열의 크기가 최대 100만이기 때문에 최대 O(nlogn)으로 문제를 해결해야 한다.
기존의 주어진 테스트 케이스보다 역추적을 해야하는 이유를 이해하기 쉬운 다음의 예제를 그림으로 살펴보자.
n = 6
A = [1, 3, 4, 5, 2, 3]
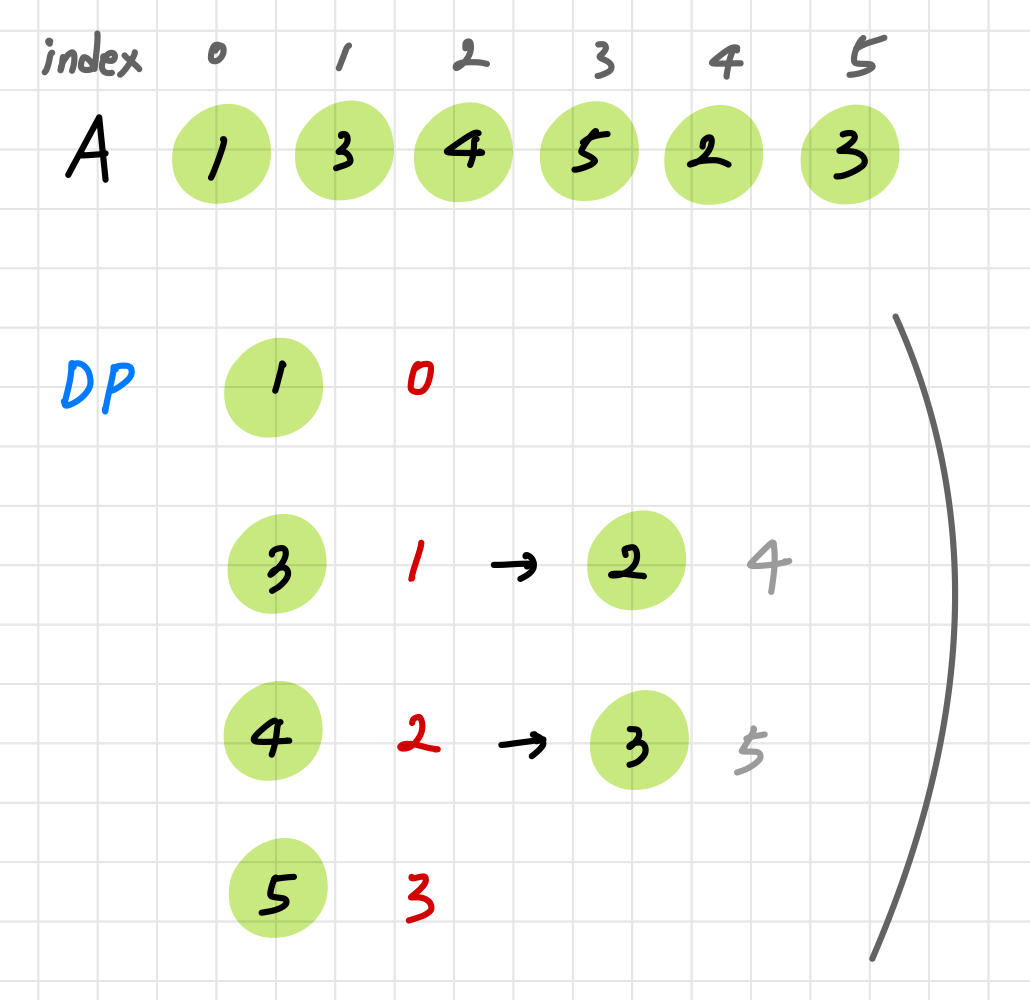
단순히 이분 탐색만을 사용해 현재 확인하고 있는 원소의 위치로 DP를 갱신할 경우, 가장 긴 증가하는 부분 수열의 길이는 정확히 계산되지만, 실제 수열을 복원하지 못하게 된다. 예를 들어, 위 그림과 같이 3은 2로, 4는 5로 갱신돼 올바른 결과인 [1, 3, 4, 5] 대신 [1, 2, 3, 5]와 같이 잘못된 수열이 나오게 되기 때문이다.
이는 이분 탐색으로 DP를 갱신하는 과정에서 실제 LIS를 구성하는 원소 간의 연결 정보를 저장하지 않기 때문이다.
따라서, 각 원소 A[i]의 이전 원소가 무엇인지 저장하는 추가적인 배열이 필요하다.
각 원소가 LIS에서 어떤 원소 뒤에 오는지를 기록하고, 마지막 원소부터 역추적해야 올바른 LIS를 복원할 수 있다.
다음과 같은 로직으로 LIS를 구할 수 있다.
1. 각 원소에 대해 이진탐색을 통해 dp에 들어갈 위치(pos)를 찾는다.
2. 위치가 dp의 끝이면 현재 가장 큰 숫자이기 때문에 추가하고, 아니면 기존값을 대체해 dp를 업데이트한다.
3. last_idx와 parent를 업데이트해 각 값의 원래 위치와 연결 관계를 기록한다.
- last_idx 배열은 dp의 각 위치에 대응하는 실제 인덱스를 저장한다.
- parent 배열은 LIS를 역추적하기 위한 연결 정보를 담는다.
위의 예제에서는 각 단계마다 다음과 같이 업데이트 된다.
| a[i] | dp | last_idx | parent[i] |
| 1 | [1] | [0] | -1 |
| 3 | [1, 3] | [0, 1] | 0 |
| 4 | [1, 3, 4] | [0, 1, 2] | 1 |
| 5 | [1, 3, 4, 5] | [0, 1, 2, 3] | 2 |
| 2 | [1, 2, 4, 5] | [0, 4, 2, 3] | 0 |
| 3 | [1, 2, 3, 5] | [0, 4, 5, 3] | 4 |
시간 복잡도: O(nlogn)
- 이분 탐색을 통한 DP 갱신: O(nlogn)
- LIS 역추적: O(n)
-> 전체 시간복잡도: O(nlogn) + O(n) = O(nlogn)
코드
from bisect import bisect_left
n = int(input())
a = list(map(int, input().split()))
dp = [] # LIS 저장 배열
parent = [-1] * n # 각 원소의 이전 원소 인덱스
last_idx = [-1] * (n+1) # LIS에서 마지막 원소의 인덱스 저장
for i, num in enumerate(a):
pos = bisect_left(dp, num) # num이 들어갈 위치
if pos == len(dp):
dp.append(num) # LIS 배열에 새로 추가
else:
dp[pos] = num # LIS 배열 갱신
last_idx[pos] = i # pos 위치의 원소 인덱스 저장
if pos > 0:
parent[i] = last_idx[pos - 1] # 이전 원소의 인덱스 저장
# 역추적해 LIS 복원
lis = []
temp = last_idx[len(dp) - 1] # 마지막 원소의 위치
while temp != -1:
lis.append(a[temp])
temp = parent[temp]
print(len(lis))
print(*lis[::-1])
간단하게 이분탐색만으로 해결이 가능했던 아래의 문제들과 달리 해당 문제는 이전 원소의 인덱스를 저장해 역추적해야했기 때문에 까다로운 문제였다. 매번 역추적 문제가 나오면 헤매는 경향이 있는데 역추적 문제를 좀 더 연습해야할 것 같다.
문제
난이도: 플레티넘 5
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구해야 한다.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.

다음과 같이 가장 긴 증가하는 부분 수열 시리즈가 있다.
LIS (Longest Increasing Subsequence) 알고리즘은 가장 긴 증가하는 부분 수열을 찾는 문제를 해결하는 알고리즘으로 주어진 수열에서 순서를 유지하면서, 원소들이 증가하는 부분 수열 중 가장 긴 수열을 찾아내는 것을 목표로 한다.
만약 해당 알고리즘이 생소하다면 위 시리즈를 순서대로 풀어보는 것을 추천한다.
알고리즘에 대한 설명은 이 영상에서 가장 쉽게 설명하는 것 같아 첫 문제부터 방향이 전혀 잡히지 않는다면 해당 영상을 먼저 보는 걸 권장한다.
풀이 과정
풀이 시간: 1시간 40분
알고리즘: 이분 탐색 + 다이나믹 프로그래밍
수열의 크기가 최대 100만이기 때문에 최대 O(nlogn)으로 문제를 해결해야 한다.
기존의 주어진 테스트 케이스보다 역추적을 해야하는 이유를 이해하기 쉬운 다음의 예제를 그림으로 살펴보자.
n = 6
A = [1, 3, 4, 5, 2, 3]

단순히 이분 탐색만을 사용해 현재 확인하고 있는 원소의 위치로 DP를 갱신할 경우, 가장 긴 증가하는 부분 수열의 길이는 정확히 계산되지만, 실제 수열을 복원하지 못하게 된다. 예를 들어, 위 그림과 같이 3은 2로, 4는 5로 갱신돼 올바른 결과인 [1, 3, 4, 5] 대신 [1, 2, 3, 5]와 같이 잘못된 수열이 나오게 되기 때문이다.
이는 이분 탐색으로 DP를 갱신하는 과정에서 실제 LIS를 구성하는 원소 간의 연결 정보를 저장하지 않기 때문이다.
따라서, 각 원소 A[i]의 이전 원소가 무엇인지 저장하는 추가적인 배열이 필요하다.
각 원소가 LIS에서 어떤 원소 뒤에 오는지를 기록하고, 마지막 원소부터 역추적해야 올바른 LIS를 복원할 수 있다.
다음과 같은 로직으로 LIS를 구할 수 있다.
1. 각 원소에 대해 이진탐색을 통해 dp에 들어갈 위치(pos)를 찾는다.
2. 위치가 dp의 끝이면 현재 가장 큰 숫자이기 때문에 추가하고, 아니면 기존값을 대체해 dp를 업데이트한다.
3. last_idx와 parent를 업데이트해 각 값의 원래 위치와 연결 관계를 기록한다.
- last_idx 배열은 dp의 각 위치에 대응하는 실제 인덱스를 저장한다.
- parent 배열은 LIS를 역추적하기 위한 연결 정보를 담는다.
위의 예제에서는 각 단계마다 다음과 같이 업데이트 된다.
| a[i] | dp | last_idx | parent[i] |
| 1 | [1] | [0] | -1 |
| 3 | [1, 3] | [0, 1] | 0 |
| 4 | [1, 3, 4] | [0, 1, 2] | 1 |
| 5 | [1, 3, 4, 5] | [0, 1, 2, 3] | 2 |
| 2 | [1, 2, 4, 5] | [0, 4, 2, 3] | 0 |
| 3 | [1, 2, 3, 5] | [0, 4, 5, 3] | 4 |
시간 복잡도: O(nlogn)
- 이분 탐색을 통한 DP 갱신: O(nlogn)
- LIS 역추적: O(n)
-> 전체 시간복잡도: O(nlogn) + O(n) = O(nlogn)
코드
from bisect import bisect_left n = int(input()) a = list(map(int, input().split())) dp = [] # LIS 저장 배열 parent = [-1] * n # 각 원소의 이전 원소 인덱스 last_idx = [-1] * (n+1) # LIS에서 마지막 원소의 인덱스 저장 for i, num in enumerate(a): pos = bisect_left(dp, num) # num이 들어갈 위치 if pos == len(dp): dp.append(num) # LIS 배열에 새로 추가 else: dp[pos] = num # LIS 배열 갱신 last_idx[pos] = i # pos 위치의 원소 인덱스 저장 if pos > 0: parent[i] = last_idx[pos - 1] # 이전 원소의 인덱스 저장 # 역추적해 LIS 복원 lis = [] temp = last_idx[len(dp) - 1] # 마지막 원소의 위치 while temp != -1: lis.append(a[temp]) temp = parent[temp] print(len(lis)) print(*lis[::-1])
간단하게 이분탐색만으로 해결이 가능했던 아래의 문제들과 달리 해당 문제는 이전 원소의 인덱스를 저장해 역추적해야했기 때문에 까다로운 문제였다. 매번 역추적 문제가 나오면 헤매는 경향이 있는데 역추적 문제를 좀 더 연습해야할 것 같다.
