[Level 3] 억억단을 외우자(Python)
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제
1억 x 1억 크기의 행렬이 주어진다.
s보다 크거나 같고 e보다 작거나 같은 수 중에서 억억단에서 가장 많이 등장한 수를 답해야 한다.
만약 가장 많이 등장한 수가 여러 개라면 그 중 가장 작은 수를 답해야 한다.
<제한 사항>
- 1 ≤ e ≤ 5,000,000
- 1 ≤ starts의 길이 ≤ min {e,100,000}
- 1 ≤ starts의 원소 ≤ e
- starts에는 중복되는 원소가 존재하지 않는다.
풀이 과정
풀이 시간: 2시간 이상
알고리즘: 수학, 누적합
이 문제의 경우, e가 최대 5,000,000이기 때문에 시간복잡도 O(NlogN)에 해결하는 것이 핵심이다.
(파이썬의 경우 1초 약 2,000만 번의 연산 횟수를 가지기 때문에)
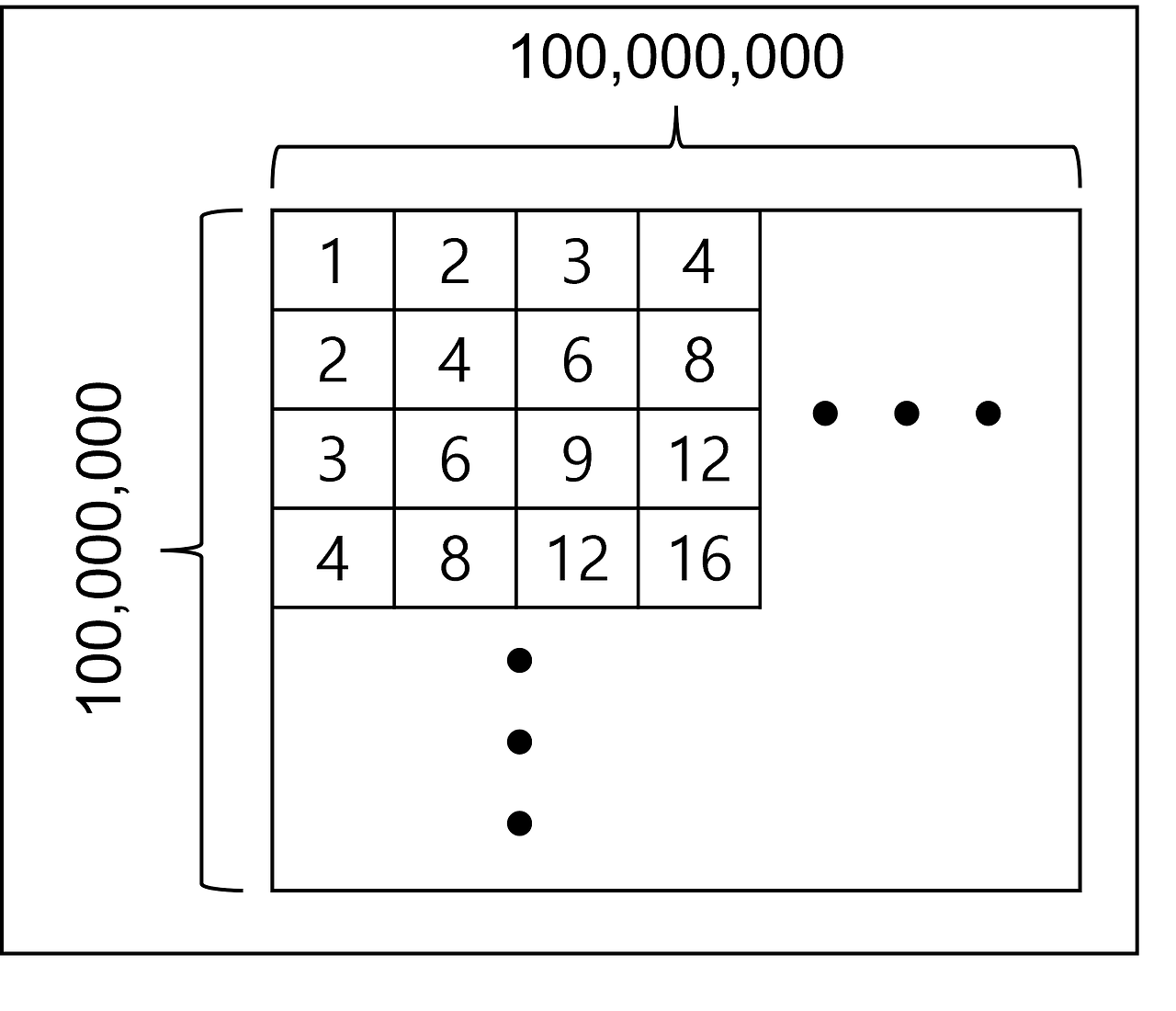
해당 이미지를 보면 파악할 수 있듯이, 억억단에 특정 범위의 숫자들이 각각 몇 번 등장했는지는 약수의 개수와 관련이 있다.
이해를 돕기 위해, 예제로 주어진 [1, 8] 구간의 각 숫자가 몇 단에서 등장하는지 살펴보자!
- 1: 1 -> 1개
- 2: 1, 2 -> 2개
- 3: 1, 3 -> 2개
- 4: 1, 2, 4 -> 3개
- 5: 1, 2, 5 -> 3개
- 6: 1, 2, 3, 6 -> 4개
- 7: 1, 7 -> 2개
- 8: 1, 2, 4, 8 -> 4개
즉, 어떤 숫자 num이 억억단에서 등장한 횟수는 약수의 개수와 같다.
그렇다면 약수의 개수는 어떻게 구할까?
쉽게 떠올릴 수 있는 방법은 1~num까지의 수를 확인하며 num이 나누어 떨어진다면 해당 숫자는 num의 약수일 것이다.
코드로 표현하면 다음과 같이 구현할 수 있다.
# 1~num까지 확인하며 약수를 구하는 방법
def find_divisors(num):
divisors = []
for i in range(1, num+1):
if num % i == 0:
divisors.append(i)
return divisors하지만, 이렇게 약수를 구한다면 어떤 수의 약수를 구하는 데 시간 복잡도는 O(num)이 되며,
최악의 경우 e(=5,000,000)에 대한 약수의 개수를 구할 때 O(e^2)이 되어 시간초과가 날 수 밖에 없다.
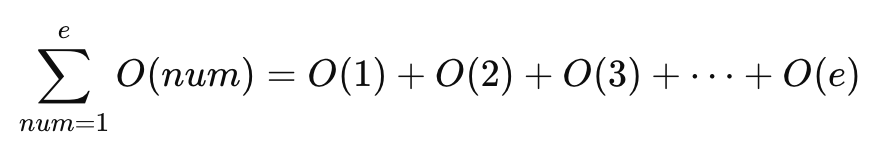
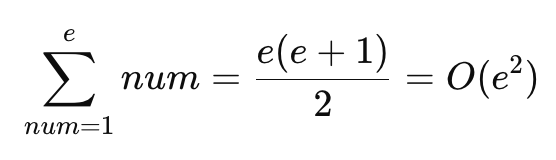
이 문제는 결국 약수의 개수를 어떻게 최적화해서 구할 수 있냐인데, 이 때 우리는 '배수의 성질'을 사용할 수 있다.
두 자연수 N = AB를 만족하는 자연수 A, B를 N의 약수라고 한다.
N = 12일때, 약수는 다음과 같이 각각의 짝이 존재한다. (1 x 12, 2 x 6, 3 x 4)
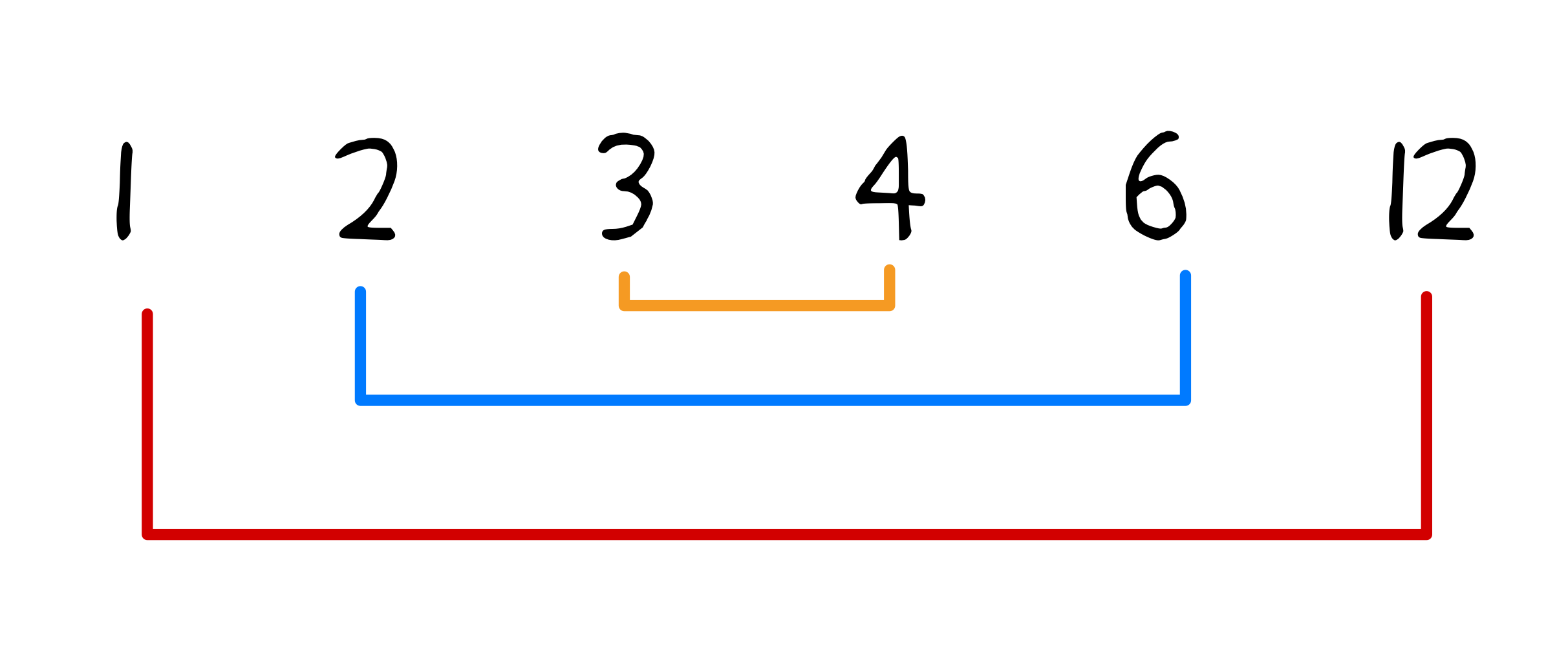
이 말인 즉슨, 우리는 1~N까지 확인할 필요없이 루트 N까지만 확인하면 된다는 것을 알 수 있다.
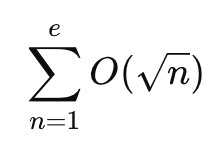

문제는 이렇게 루트 e까지만 확인하더라도 여전히 1~e까지 모든 숫자에 대한 약수의 개수를 계산하면
여전히 시간복잡도는 O(e^3/2)로 시간초과가 난다.
이 배수의 개념을 좀 더 확장해 나간다면 아마 아래의 코드까지 도달할 수 있을지도 모른다.
def find_divisors(num):
divisors = [0] * (num+1)
for i in range(2, num+1):
for j in range(1, num // i + 1):
divisors[i * j] += 1
return divisors하지만, 이 역시 반복문의 횟수는 n/1 + n/2 + n/3 + ... + n/n으로
1 + 1/2 + 1/3 + ... 1/n와 같고 이는 log(n)+1 이하의 시간복잡도를 갖는다고 할 수 있다. (조화급수)
결과적으로 줄여도 O(e * log(e))로 연산 횟수는 여전히 최악의 경우 약 111,267,483번이 되어 시간초과가 발생한다.
이쯤되면, 숨이 '억'하고 막혀서 '억억단'일지도 모른다 🫢
하지만, 결국 위에서 살펴 본 '제곱근까지만 확인하면 된다'는 점과 '배수의 성질'을 계속해서 확장해나가면
최종적으로 O(e**0.5 * loge)까지 시간복잡도를 줄일 수 있다!
def find_divisors(num: int) -> list:
"""
:param num: 문제에서 주어진 e
:return: 1이상 num 이하의 모든 수들에 대한 약수의 개수 배열
"""
divisors = [0] * (num + 1)
for i in range(1, int(num ** 0.5) + 1):
# i의 제곱인 i*i는 약수로 자기 자신을 포함(제곱수의 경우, 약수의 개수가 홀수)
divisors[i * i] += 1
# i와 j // i는 약수가 되므로 2씩 증가
for j in range(i * (i + 1), num + 1, i):
divisors[j] += 2
return divisors
코드와 같이
1 ~ 루트 num까지의 숫자만 확인해 루트 num ~ num의 배수의 개수도 한번에 구할 수 있다는 말이다.
예를 들어, num으로 8이 주어졌다고 가정해보자.
divisors를 [0, 0, 0, 0, 0, 0, 0, 0, 0]로 초기화 한 후
1부터 num의 제곱근인 2까지만 확인하며 해당 수로 만들 수 있는 배수를 카운트 하는 것이다.
이 때, 제곱근은 항상 자기 자신을 포함해 약수의 개수가 홀수이기 때문에 i * i는 +1을 추가로 해준다. (짝이 없는 경우기 때문에)
i = 1일 때, j=1*2=2부터 8까지 1만큼 증가시키면서 확인한다면 1을 약수로 갖는 모든 수에 약수의 개수를 추가해주는 것과 같다.
즉, j는 i를 약수로 갖는 수라고 생각하면 된다.
i = 1 -> j = 1 ~ 8까지 모든 수가 1과 자기 자신을 약수로 갖기 때문에 +2를 해준다.
i = 2 -> 2*2=4(제곱수)의 경우 자기 자신을 약수로 갖기 때문에 +1을 해주고, j = 2*3부터 ~ 2*4=8까지 2를 약수로 갖는 수 6, 8에 대해 약수의 개수를 또 +2 해준다.
이렇게 구현한다면 결국, O(e**0.5 * loge)까지 시간복잡도를 최대로 줄일 수 있다.
이후 문제는 이 약수의 개수를 통해 각 구간에 대해 어떻게 가장 많이 등장한 수를 찾느냐인데?
구간에 관한 언급이 나오면 누적 빈도 배열을 고려해봐야 한다.
most_freq = [0] * (e + 1)
max_num = e # 현재까지 발견된 최대 약수 개수를 가진 숫자
for i in range(e, 0, -1):
# 현재 숫자의 약수 개수가 더 많거나, 약수 개수가 같은 경우 더 작은 숫자 선택
if divisor_cnt[i] >= divisor_cnt[max_num]:
max_num = i
most_freq[i] = max_num
약수의 개수 배열을 역순으로 탐색하면서(작은 숫자부터 시작하면 이후의 숫자들을 고려할 때 다시 이전의 숫자들을 확인해야 하기 때문)
만약 현재 확인하고 있는 숫자가 같거나 더 많은 약수의 개수를 갖는 경우, 해당 숫자의 약수의 개수를 most_freq 배열에 업데이트 해준다.
그럼 결국 아래와 같이 전체 시간복잡도를 구할 수 있다.
시간 복잡도
- find_divisors 함수: O(sqrt(num) * (num/i)) = O(num * sqrt(num)) = O(e**0.5 * log(e))
- 역순 탐색: O(e)
- 결과확인: O(len(starts))
→ 전체 시간복잡도: O(e⋅sqrt(e))+O(e)+O(k)
코드
def find_divisors(num: int) -> list:
"""
:param num: 문제에서 주어진 e
:return: 1이상 num 이하의 모든 수들에 대한 약수의 개수 배열
"""
divisors = [0] * (num + 1)
for i in range(1, int(num ** 0.5) + 1):
# i의 제곱인 i*i는 약수로 자기 자신을 포함(제곱수의 경우, 약수의 개수가 홀수)
divisors[i * i] += 1
# i와 j // i는 약수가 되므로 2씩 증가
for j in range(i * (i + 1), num + 1, i):
divisors[j] += 2
return divisors
def solution(e: int, starts: list) -> list:
# 1. 1 ~ e까지 전체 약수의 개수(등장한 횟수) 계산
divisor_cnt = find_divisors(e)
# 2. 누적 빈도 배열을 사용해 특정 구간 내에서 가장 많이 등장한 수 찾기
most_freq = [0] * (e + 1)
max_num = e # 현재까지 발견된 최대 약수 개수를 가진 숫자
for i in range(e, 0, -1):
# 현재 숫자의 약수 개수가 더 많거나, 약수 개수가 같은 경우 더 작은 숫자 선택
if divisor_cnt[i] >= divisor_cnt[max_num]:
max_num = i
most_freq[i] = max_num
return [most_freq[s] for s in starts]
약수의 개수를 구하는 부분의 시간복잡도를 줄이기 위해 굉장히 많은 시간을 쓴 문제다.
실제로 이 문제의 경우, find_divisors 함수를 O(eloge)로만 작성해도 C++나 Java는 통과가 된다고 하기도 하는데
Python의 경우, 테스트 케이스 10번에서 안정적으로 통과되지 않았다.
하지만, 위와 같이 약수의 개수를 O(e**0.5 * loge)까지 줄이고 나서는 10번 테스트 케이스도 안정적으로 5초내로 통과할 수 있었다.
이와 관련해서 약수 및 배수의 성질을 활용한 문제를 풀어보고 싶다면 백준의 약수의 합을추천한다.